This is a brief summary of ML course provided by Andrew Ng and Stanford in Coursera.
You can find the lecture video and additional materials in
https://www.coursera.org/learn/machine-learning/home/welcome
Coursera | Online Courses From Top Universities. Join for Free
1000+ courses from schools like Stanford and Yale - no application required. Build career skills in data science, computer science, business, and more.
www.coursera.org
Feature Scaling
Idea: Make sure feautres are on a similiar scale.
e.g., $x_1$ = size (0 - 2000 $ft^2$, $x_2$ = number of bedrooms (1-5)
It can take a long time to find the way to the global minimum, if you run gradient descents on this funcion.
$x_1 = frac{size}{2000}, x_2 = frac{num of bedrooms}{5}$
But if you scale as above, you can find a much more direct path to the global minimum rather than taking a much more convoluted path where you are sorty of trying to follow a much more complicated trajectory to get to the global min.
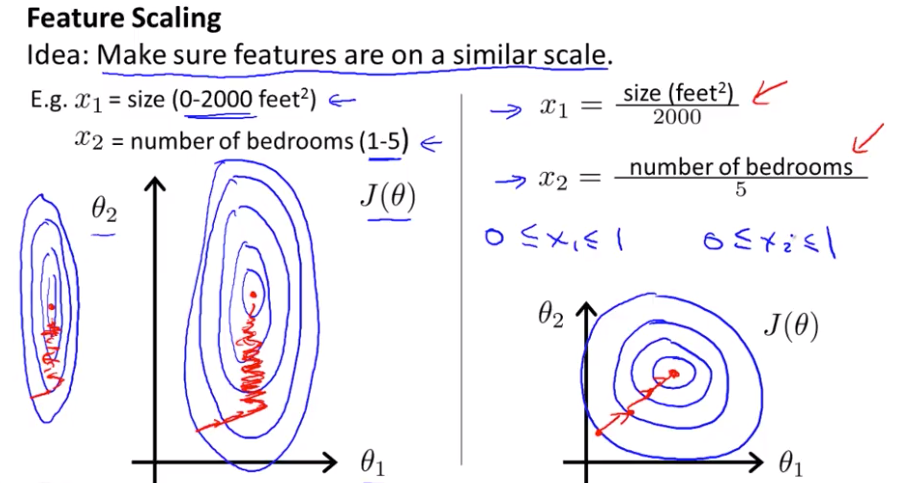
Get every feature into approximately a $-1 \leq x_i \leq 1$ range.

Mean Normalization
Replace $x_i$ with $x_i - \mu_i$ to make features have approximately zero mean (Do not apply to $x_0$ = 1).
e.g., $x_1 = \frac{size-1000}{2000}$, $x_2 = \frac{num of bedrooms - 2}{5}$
-> $ -0.5 \leq x_1 \leq 0,5, -0.5 \leq x_2 \leq 0.5$

Quiz: Suppose you are using a learning algorithm to estimate the price of houses in a city. You want one of your features $x_i$ to capture the age of the house. In your training set, all of your houses have an age between 30 and 50 years, with an average age of 38 years. Which of the following would you use as features, assuming you use feature scaling and mean normalization?
Answer: $\frac{age of house-38}{20}$
Lecturer's Note
We can speed up gradient descent by having each of our input values in roughly the same range. This is because θ will descend quickly on small ranges and slowly on large ranges, and so will oscillate inefficiently down to the optimum when the variables are very uneven.
The way to prevent this is to modify the ranges of our input variables so that they are all roughly the same. Ideally:
$ -1 \leq x_{(i)} \leq 1 $
$ -0.5 \leq x_{(i)} \leq 0.5 $
These aren't exact requirements; we are only trying to speed things up. The goal is to get all input variables into roughly one of these ranges, give or take a few.
Two techniques to help with this are feature scaling and mean normalization. Feature scaling involves dividing the input values by the range (i.e. the maximum value minus the minimum value) of the input variable, resulting in a new range of just 1. Mean normalization involves subtracting the average value for an input variable from the values for that input variable resulting in a new average value for the input variable of just zero. To implement both of these techniques, adjust your input values as shown in this formula:
$x_i := \frac{x_i - \mu_i}{s_i}$
where $\mu_i$ is the average of all the values for feature (i) and $s_i$ is the range of values (max - min) or $s_i$ is the standard deviation.
Note that dividing by the range, or dividing by the standard deviation, give different results. The quizzes in this course use range - the programming exercises use standard deviation.
For example, if $x_i$ represents housing prices with a range of 100 to 2000 and a mean value of 1000, then, $x_i := \frac{price - 1000}{1900}$.



