This is a brief summary of ML course provided by Andrew Ng and Stanford in Coursera.
You can find the lecture video and additional materials in
https://www.coursera.org/learn/machine-learning/home/welcome
Coursera | Online Courses From Top Universities. Join for Free
1000+ courses from schools like Stanford and Yale - no application required. Build career skills in data science, computer science, business, and more.
www.coursera.org
Gradient Descent
$\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)$
- "Debugging": how to make sure gradient descent is working correctly.
- how to choose learning rate $\alpha$
Making sure gradient descent is working correctly.
$min_{\theta} J(\theta)$ should decreases as the num of iteration increases.
if $j_{\theta}$ is increasing try to use smaller $\alpha$


Quiz: Suppose a friend ran gradient descent three times, with α=0.01, α=0.1, and α=1, and got the following three plots (labeled A, B, and C):
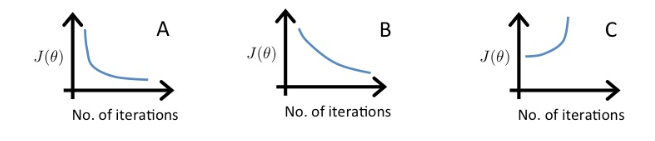
Which plots corresponds to which values of $\alpha$?
Answer:
A is α=0.1. B is α=0.01, C is α=1.
In graph C, the cost function is increasing, so the learning rate is set too high. Both graphs A and B converge to an optimum of the cost function, but graph B does so very slowly, so its learning rate is set too low. Graph A lies between the two.
Summary:
- if $\alpha$ is too small: slow convergence.
- if $\alpha$ is too large: $J(\theta)$ may not decrease on every iteration; may not converge.
To choose $\alpha$, try ..., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, ... (3X times from the previous values)
Lecturer's Note
Debugging gradient descent. Make a plot with number of iterations on the x-axis. Now plot the cost function, J(θ) over the number of iterations of gradient descent. If J(θ) ever increases, then you probably need to decrease α.
Automatic convergence test. Declare convergence if J(θ) decreases by less than E in one iteration, where E is some small value such as 10−3. However in practice it's difficult to choose this threshold value.
It has been proven that if learning rate α is sufficiently small, then J(θ) will decrease on every iteration.
To summarize:
If α is too small: slow convergence.
If α is too large: may not decrease on every iteration and thus may not converge.



