[Machine Learning by Stanford] Solving the Problem of Overfitting - Regularized Logistic Regression

This is a brief summary of ML course provided by Andrew Ng and Stanford in Coursera.

You can find the lecture video and additional materials in 

https://www.coursera.org/learn/machine-learning/home/welcome

Coursera | Online Courses From Top Universities. Join for Free

Adapt both gradient descent and the more advanced optimization techniques in order to have them work for regularized logistic regression.

 

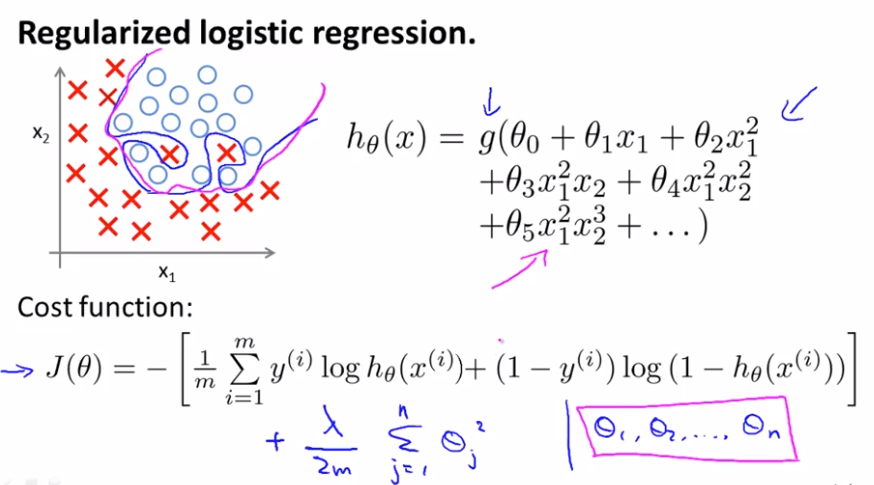
With a lot of features, you can end up with overtfitting for logistic regression problems. 

New cost function below will give you the effect that even though you are fitting a very high order polynomial with a lot of params, so long as you apply regularization, and keep the params small, you are more likely to get a decision boundary, more reasonably separating the positive and the negative examples. 

 

Quiz: When using regularized logistic regression, which of these is the best way to monitor whether gradient descent is working correctly?

 

Answer: c

 

Cost functions need to return were first J-val (need to compute the cost function J of theta) 

 

Lecturer's Note

Regularized Logistic Regression

We can regularize logistic regression in a similar way that we regularize linear regression. As a result, we can avoid overfitting. The following image shows how the regularized function, displayed by the pink line, is less likely to overfit than the non-regularized function represented by the blue line:

 

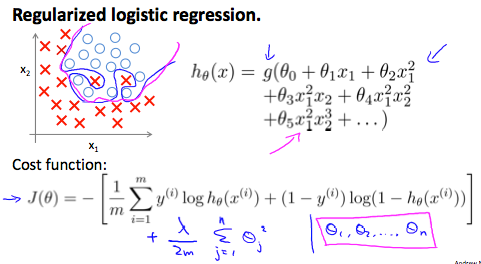
Cost Function

Recall that our cost function for logistic regression was:

$J(\theta) = - \frac{1}{m}\sum_{i=1}^m [y^{(i)} log (h_{\theta} (x^{(i)}) + (1-y^{(i)}) log ( 1 - h_{\theta}(x^{(i)}))]$ 

We can regularize this equation by adding a term to the end:

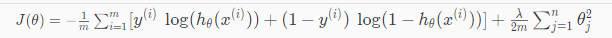
The second sum, $\sum_{j=1}^n \theta_j^2$ means to explicitly exclude the bias term, θ0​. I.e. the θ vector is indexed from 0 to n (holding n+1 values, θ0​ through θn​), and this sum explicitly skips θ0​, by running from 1 to n, skipping 0. Thus, when computing the equation, we should continuously update the two following equations: