This is a brief summary of ML course provided by Andrew Ng and Stanford in Coursera.
You can find the lecture video and additional materials in
https://www.coursera.org/learn/machine-learning/home/welcome
Coursera | Online Courses From Top Universities. Join for Free
1000+ courses from schools like Stanford and Yale - no application required. Build career skills in data science, computer science, business, and more.
www.coursera.org
1. You are training a classification model with logistic regression. Which of the following statements are true? Check
all that apply.
a. Introducing regularization to the model always results in equal or better performance on examples not in the training set.
b. Adding many new features to the model makes it more likely to overfit the training set.
c. Adding a new feature to the model always results in equal or better performance on examples not in the training set.
d. Introducing regularization to the model always results in equal or better performance on the training set.
Answer: b
2. Suppose you ran logistic regression twice, once with λ=0, and once with λ=1. One of the times, you got parameters θ=[26.29 65.41], and the other time you got θ=[2.75 1.32]. However, you forgot which value of λ corresponds to which value of θ. Which one do you think corresponds to λ=1?
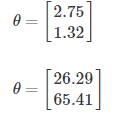
Answer: a
Explanation: when lambda is set to 1, we use regularization to penalize large values of theta. Thus, the params, theta, obtained will in general have smaller values.
3. Which of the following statements about regularization are true? Check all that apply.
a. Using too large a value of λ can cause your hypothesis to underfit the data.
b. Because logistic regression outputs values $ 0 \leq h_\theta(x) \leq 1 $, its range of output values can only be "shrunk" slightly by regularization anyway, so regularization is generally not helpful for it.
c. Because regularization causes J(θ) to no longer be convex, gradient descent may not always converge to the global minimum (when λ>0, and when using an appropriate learning rate α).
d. Using a very large value of λ cannot hurt the performance of your hypothesis; the only reason we do not set λ to be too large is to avoid numerical problems.
Answer: a
4. In which one of the following figures do you think the hypothesis has overfit the training set?

Answer: a
5. In which one of the following figures do you think the hypothesis has underfit the training set?

Answer: a
6.
Which of the following statements about regularization are true? Check all that apply.
a. Using too large a value of \lambdaλ can cause your hypothesis to overfit the data; this can be avoided by reducing λ.
b. Consider a classification problem. Adding regularization may cause your classifier to incorrectly classify some training examples (which it had correctly classified when not using regularization, i.e. when λ=0).
c. Using a very large value of \lambdaλ cannot hurt the performance of your hypothesis; the only reason we do not set λ to be too large is to avoid numerical problems.
d. Because logistic regression outputs values 0 $ 0 \leq h_\theta(x) \leq 1 $, its range of output values can only be "shrunk" slightly by regularization anyway, so regularization is generally not helpful for it.
Answer: a, b



